Note
Go to the end to download the full example code
Compare topographies
This example shows how to compare EEG topographies, based on the method described by McCarthy & Wood [1].
# sphinx_gallery_thumbnail_number = 4
from eelbrain import *
Simulated data
Generate a simulated dataset (as in the T-test example)
dss = []
for subject in range(10):
# generate data for one subject
ds = datasets.simulate_erp(seed=subject)
# average across trials to get condition means
ds_agg = ds.aggregate('predictability')
# add the subject name as variable
ds_agg[:, 'subject'] = f'S{subject:02}'
dss.append(ds_agg)
ds = combine(dss)
# make subject a random factor (to treat it as random effect for ANOVA)
ds['subject'].random = True
# Re-reference the EEG data (i.e., subtract the mean of the two mastoid channels):
ds['eeg'] -= ds['eeg'].mean(sensor=['M1', 'M2'])
print(ds.head())
# n cloze predictability n_chars subject
-----------------------------------------------------
0 40 0.88051 high 5 S00
1 40 0.17241 low 5 S00
2 40 0.89466 high 4.95 S01
3 40 0.13778 low 4.975 S01
4 40 0.90215 high 5.05 S02
5 40 0.12206 low 4.975 S02
6 40 0.88503 high 5.2 S03
7 40 0.14273 low 4.875 S03
8 40 0.90499 high 5.075 S04
9 40 0.15732 low 5.025 S04
-----------------------------------------------------
NDVars: eeg
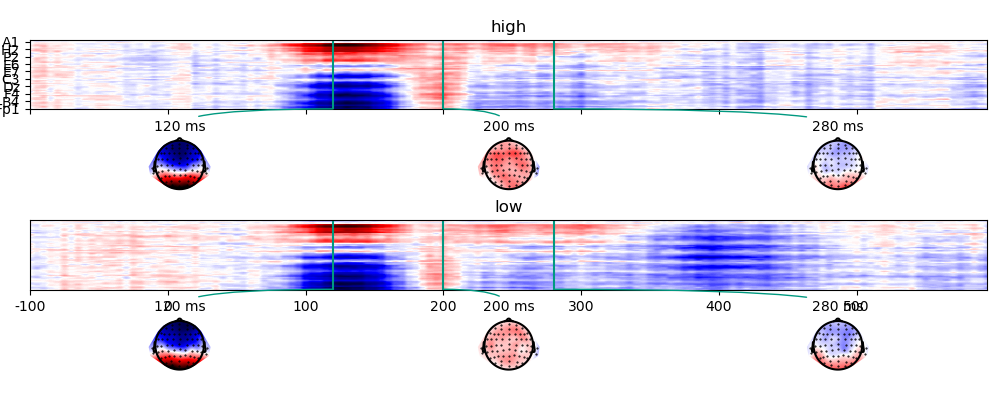
The simulated data in the two conditions:
p = plot.TopoArray('eeg', 'predictability', data=ds, columns=1, axh=2, axw=10, t=[0.120, 0.200, 0.280], head_radius=0.35)
Test between conditions
Test whether the 120 ms topography differs between the two cloze conditions. The dataset already includes one row per cell (i.e., per cloze condition and subject). Consequently, we can just index the topography at the desired time point:
topography = ds['eeg'].sub(time=0.120)
# normalize the data in accordance with McCarth & Wood (1985)
topography = normalize_in_cells(topography, 'sensor', 'predictability', ds)
# "melt" the topography NDVar to turn the sensor dimension into a Factor
ds_topography = table.melt_ndvar(topography, 'sensor', ds=ds)
# Note EEG is a single column, and the last column indicates the sensor
ds_topography.head()
ANOVA to test whether the effect of predictability differs between sensors:
test.ANOVA('eeg', 'predictability * sensor * subject', data=ds_topography)
The non-significant interaction suggests that the effect of predictability does not differ between sensors, i.e., the topographies do not differ, which is consistent with being generated by the same underlying neural sources.
Test two time points
Since we’re not interested in condition here, we first average across conditions, i.e., with the goal of having one row per subject:
ds_average = ds.aggregate('subject', drop_bad=True)
print(ds_average)
# n cloze n_chars subject
------------------------------------
0 40 0.52646 5 S00
1 40 0.51622 4.9625 S01
2 40 0.51211 5.0125 S02
3 40 0.51388 5.0375 S03
4 40 0.53115 5.05 S04
5 40 0.52163 4.9125 S05
6 40 0.53789 5.0625 S06
7 40 0.52491 4.8625 S07
8 40 0.52464 5.2125 S08
9 40 0.52559 5 S09
------------------------------------
NDVars: eeg
In order to compare two time points, we need to construct a new dataset with time point as Factor:
dss = []
for time in [0.120, 0.280]:
ds_time = ds_average['subject',] # A new dataset with the 'subject' variable only
ds_time['eeg'] = ds_average['eeg'].sub(time=time)
ds_time[:, 'time'] = f'{time*1000:.0f} ms'
dss.append(ds_time)
ds_times = combine(dss)
ds_times.summary()
Then, normalize the data in accordance with McCarth & Wood (1985)
topography = normalize_in_cells('eeg', 'sensor', 'time', data=ds_times)
# "melt" the topography NDVar to turn the sensor dimension into a Factor
ds_topography = table.melt_ndvar(topography, 'sensor', ds=ds_times)
# Note EEG is a single column, and the last column indicates the sensor
ds_topography.head()
Plot the topographies before and after normalization:
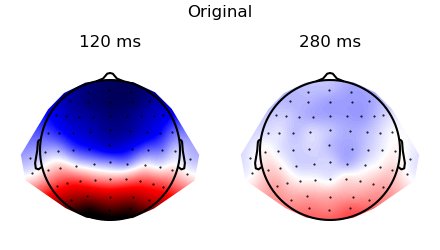
p = plot.Topomap('eeg', 'time', data=ds_times, columns=2, title="Original", head_radius=0.35)
p = plot.Topomap(topography, 'time', data=ds_times, columns=2, title="Normalized", head_radius=0.35)
Compre the topographies with the ANOVA – test whether the effect of time differs between sensors:
test.ANOVA('eeg', 'time * sensor * subject', data=ds_topography)
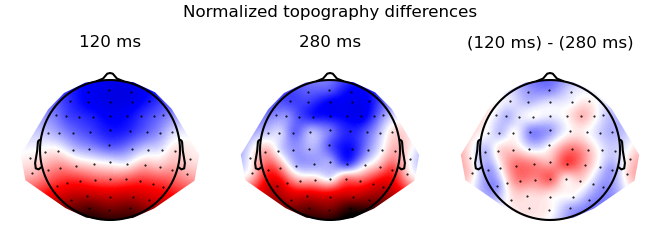
Visualize the difference
res = testnd.TTestRelated(topography, 'time', match='subject', data=ds_times)
p = plot.Topomap(res, columns=3, title="Normalized topography differences", head_radius=0.35)
Permutation test: 0%| | 0/1023 [00:00<?, ? permutations/s]
Permutation test: 100%|██████████| 1023/1023 [00:00<00:00, 11240.36 permutations/s]
References
Total running time of the script: (0 minutes 6.067 seconds)