Note
Go to the end to download the full example code
Creating NDVars
Shows how to initialize an NDVar with the structure of EEG data from
(randomly generate) data arrays. The data is intended for illustrating EEG
analysis techniques and meant to vaguely resemble data from an N400 experiment,
but it is not meant to be a physiologically realistic simulation.
# sphinx_gallery_thumbnail_number = 3
import numpy as np
import scipy.spatial
from eelbrain import *
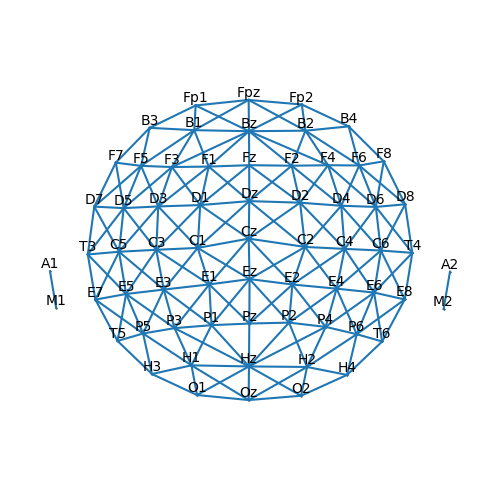
NDVars associate data arrays with Dimension objects that describe what the different data axes mean, and provide meta information thay is used, for example for plotting. Start by create a Sensor dimension from an actual montage:
sensor = Sensor.from_montage('standard_alphabetic')
p = plot.SensorMap(sensor)

The dimenson also contains information about the connectivity of its elements (i.e., specifying which elements are adjacent), which is used, for example, for cluster-based analysis. This information is imported automatically from mne-python when available; otherwise it can be defined manually when creating the sensor object, or based on distance as here:
sensor.set_connectivity(connect_dist=1.66)
p = plot.SensorMap(sensor, connectivity=True)
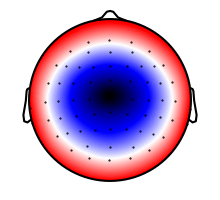
Using information from the Sensor description about sensor coordinates, we
can now generate an N400-like topography. After associating the data array
with the Sensor description by creating an NDVar, the topography can be plotted
without any further information:
i_cz = sensor.names.index('Cz')
cz_loc = sensor.locs[i_cz]
dists = scipy.spatial.distance.cdist([cz_loc], sensor.locs)[0]
dists /= dists.max()
topo = -0.7 + dists
n400_topo = NDVar(topo, sensor)
p = plot.Topomap(n400_topo, clip='circle')
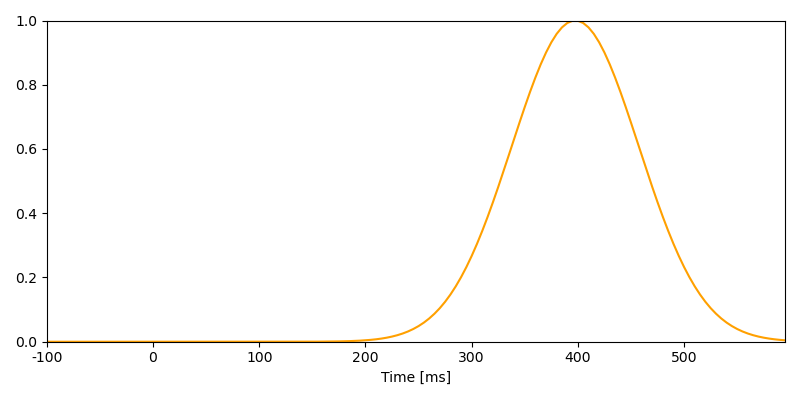
The time axis is specified using a UTS (“uniform time series”)
object. As with the topography, the UTS object allows the NDVar to
automatically format the time axis of a figure:
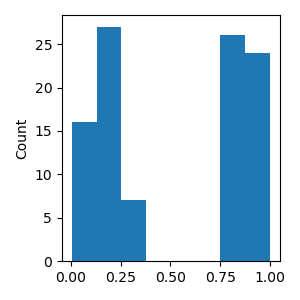
Generate random values for the independent variable (call it “cloze probability”)
rng = np.random.RandomState(0)
n_trials = 100
cloze = np.concatenate([
rng.uniform(0, 0.3, n_trials // 2),
rng.uniform(0.8, 1.0, n_trials // 2),
])
rng.shuffle(cloze)
p = plot.Histogram(cloze)
Put all the dimensions together to simulate the EEG signal. On the first
line, turn cloze into Var to make clear that cloze represents a Case
dimension, i.e. different trials (rather than data on the time dimension in
n400_timecourse):
signal = Var(1 - cloze) * n400_timecourse * n400_topo
# Add noise
noise = powerlaw_noise(signal, 1)
noise = noise.smooth('sensor', 0.02, 'gaussian')
signal += noise
# Apply the average mastoids reference
signal -= signal.mean(sensor=['M1', 'M2'])
# Store EEG data in a Dataset with trial information
ds = Dataset({
'eeg': signal,
'cloze': Var(cloze),
'predictability': Factor(cloze > 0.5, labels={True: 'high', False: 'low'}),
})
Plot the average simulated response
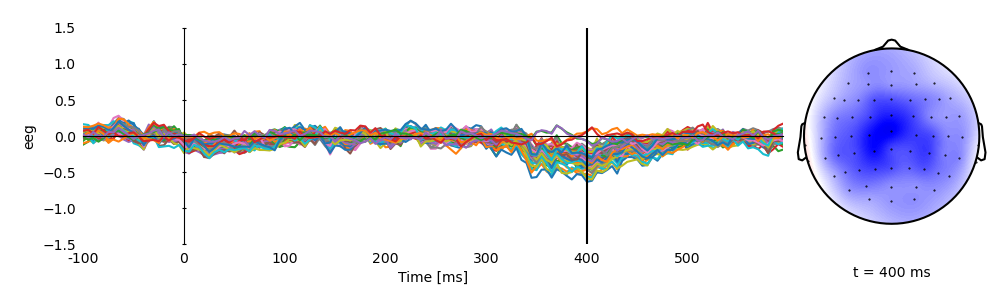
p = plot.TopoButterfly('eeg', data=ds, vmax=1.5, clip='circle', frame='t', axh=3)
p.set_time(0.400)
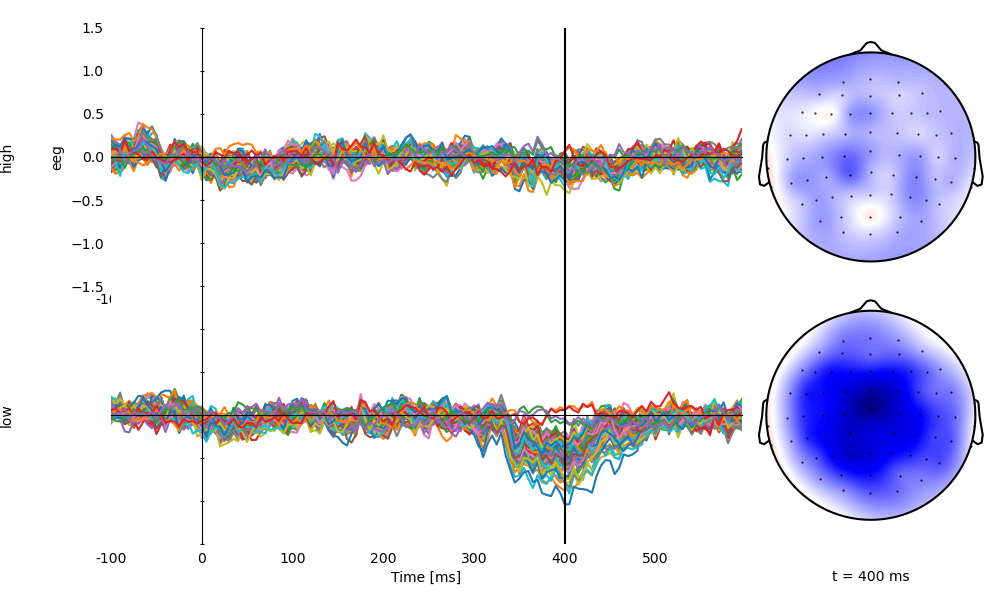
Plot averages separately for high and low cloze
p = plot.TopoButterfly('eeg', 'predictability', data=ds, vmax=1.5, clip='circle', frame='t', axh=3)
p.set_time(0.400)
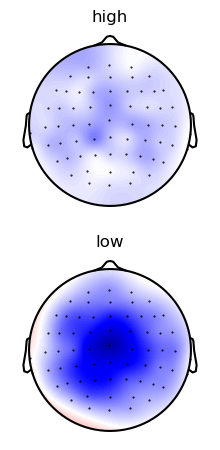
Average over time in the N400 time window
p = plot.Topomap('eeg.mean(time=(0.300, 0.500))', 'predictability', data=ds, vmax=1, clip='circle')
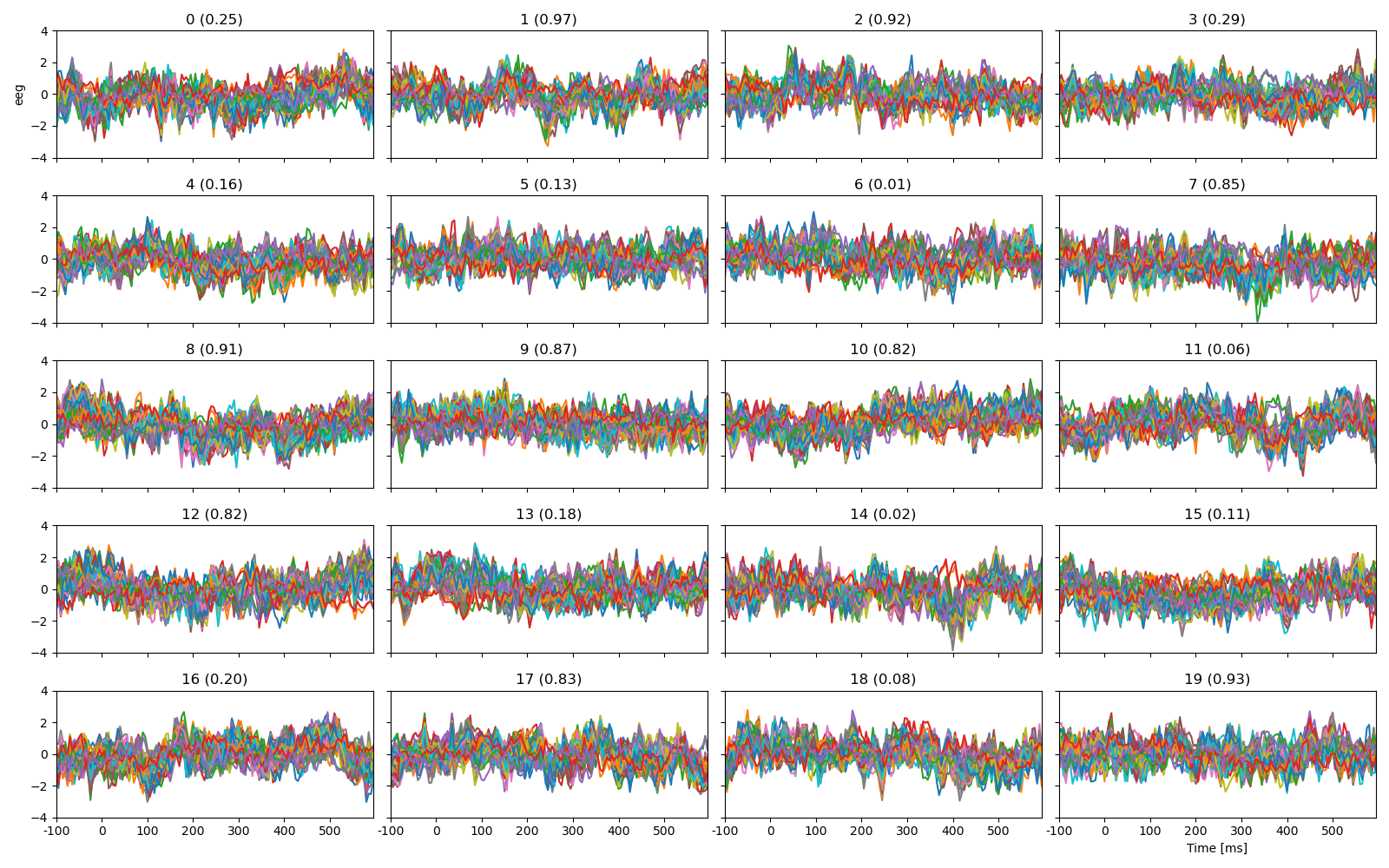
Plot the first 20 trials, labeled with cloze propability
Total running time of the script: (0 minutes 4.975 seconds)