T-test

This example show a cluster-based permutation test for a simple design (two conditions). The example uses simulated data meant to vaguely resemble data from an N400 experiment (not intended as a physiologically realistic simulation).

# sphinx_gallery_thumbnail_number = 3
from eelbrain import *

Simulated data

Each function call to datasets.simulate_erp() generates a dataset equivalent to an N400 experiment for one subject. The seed argument determines the random noise that is added to the data.

ds = datasets.simulate_erp(seed=0)
print(ds.summary())

Key              Type     Values
-------------------------------------------------------------------------
eeg              NDVar    140 time, 65 sensor; -2.54472e-05 - 2.56669e-05
cloze            Var      0.00563694 - 0.997675
predictability   Factor   high:40, low:40
n_chars          Var      3:10, 4:20, 5:22, 6:16, 7:12
-------------------------------------------------------------------------
Dataset: 80 cases

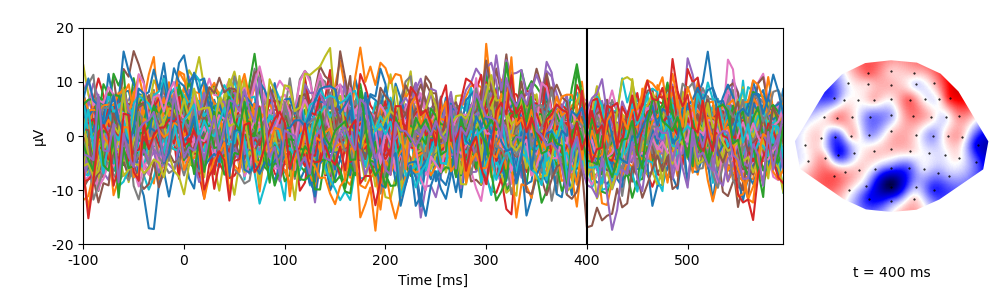
A singe trial of data:

p = plot.TopoButterfly('eeg[0]', data=ds, t=0.400)

The Dataset.aggregate() method computes condition averages when sorting the data into conditions of interest. In our case, the predictability variable specified conditions 'high' and 'low' cloze:

print(ds.aggregate('predictability'))

n    cloze     predictability   n_chars
---------------------------------------
40   0.88051   high             5
40   0.17241   low              5
---------------------------------------
NDVars: eeg

Group level data

This loop simulates a multi-subject experiment. It generates data and collects condition averages for 10 virtual subjects. For group level analysis, the collected data are combined in a Dataset:

dss = []
for subject in range(10):
    # generate data for one subject
    ds = datasets.simulate_erp(seed=subject)
    # average across trials to get condition means
    ds_agg = ds.aggregate('predictability')
    # add the subject name as variable
    ds_agg[:, 'subject'] = f'S{subject:02}'
    dss.append(ds_agg)

ds = combine(dss)
# make subject a random factor (to treat it as random effect for ANOVA)
ds['subject'].random = True
print(ds.head())

n    cloze     predictability   n_chars   subject
-------------------------------------------------
40   0.88051   high             5         S00
40   0.17241   low              5         S00
40   0.89466   high             4.95      S01
40   0.13778   low              4.975     S01
40   0.90215   high             5.05      S02
40   0.12206   low              4.975     S02
40   0.88503   high             5.2       S03
40   0.14273   low              4.875     S03
40   0.90499   high             5.075     S04
40   0.15732   low              5.025     S04
-------------------------------------------------
NDVars: eeg

Re-reference the EEG data (i.e., subtract the mean of the two mastoid channels):

ds['eeg'] -= ds['eeg'].mean(sensor=['M1', 'M2'])

Spatio-temporal cluster based test

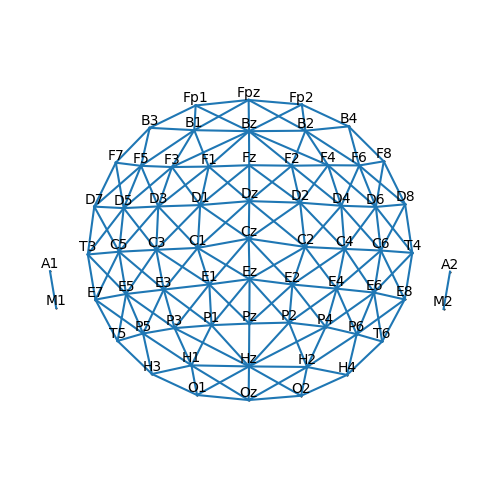
Cluster-based tests are based on identifying clusters of meaningful effects, i.e., groups of adjacent sensors that show the same effect (see testnd for references). In order to find clusters, the algorithm needs to know which channels are neighbors. This information is refered to as the sensor connectivity (i.e., which sensors are connected). The connectivity graph can be visualized to confirm that it is set correctly.

p = plot.SensorMap(ds['eeg'], connectivity=True)

With the correct connectivity, we can now compute a cluster-based permutation test for a related measures t-test:

res = testnd.TTestRelated(
    'eeg', 'predictability', 'low', 'high', match='subject', data=ds,
    pmin=0.05,  # Use uncorrected p = 0.05 as threshold for forming clusters
    tstart=0.100,  # Find clusters in the time window from 100 ...
    tstop=0.600,  # ... to 600 ms
)

Permutation test:   0%|          | 0/1023 [00:00<?, ? permutations/s]
Permutation test:  11%|█         | 111/1023 [00:00<00:00, 1101.64 permutations/s]
Permutation test:  23%|██▎       | 235/1023 [00:00<00:00, 1180.83 permutations/s]
Permutation test:  35%|███▌      | 360/1023 [00:00<00:00, 1207.29 permutations/s]
Permutation test:  48%|████▊     | 487/1023 [00:00<00:00, 1229.89 permutations/s]
Permutation test:  60%|██████    | 614/1023 [00:00<00:00, 1243.91 permutations/s]
Permutation test:  73%|███████▎  | 744/1023 [00:00<00:00, 1261.60 permutations/s]
Permutation test:  86%|████████▌ | 876/1023 [00:00<00:00, 1279.76 permutations/s]
Permutation test:  98%|█████████▊| 1004/1023 [00:00<00:00, 1278.94 permutations/s]
Permutation test: 100%|██████████| 1023/1023 [00:00<00:00, 1250.64 permutations/s]

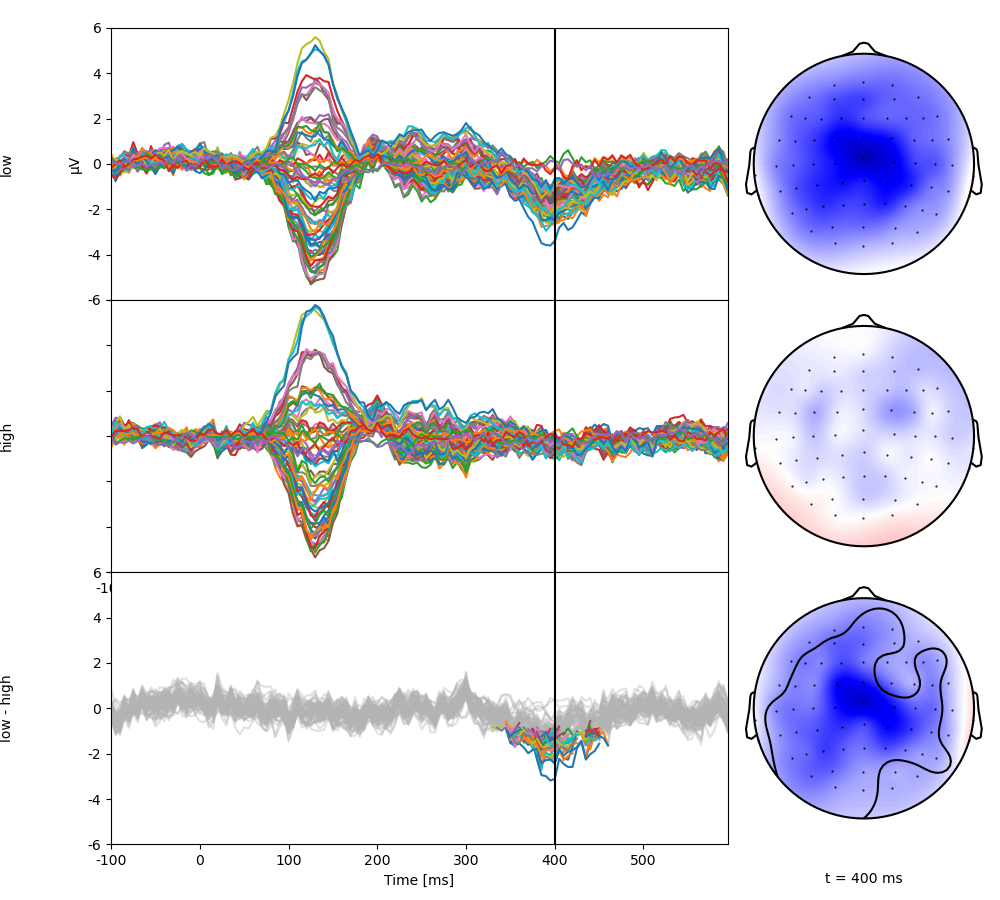
Plot the test result. The top two rows show the two condition averages. The bottom butterfly plot shows the difference with only significant regions in color. The corresponding topomap shows the topography at the marked time point, with the significant region circled (in an interactive environment, the mouse can be used to update the time point shown).

p = plot.TopoButterfly(res, clip='circle', t=0.400)

Generate a table with all significant clusters:

clusters = res.find_clusters(0.05)
clusters

id	tstart	tstop	duration	n_sensors	v	p	sig
55	0.33	0.465	0.135	55	-1677.1	0.0029326	**

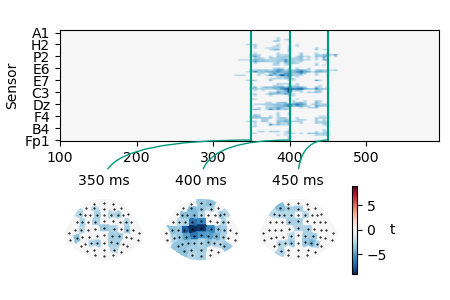
Retrieve the cluster map using its ID and visualize the spatio-temporal extent of the cluster:

cluster_id = clusters[0, 'id']
cluster = res.cluster(cluster_id)
p = plot.TopoArray(cluster, interpolation='nearest', t=[0.350, 0.400, 0.450, None])
# plot the colorbar next to the right-most sensor plot
p_cb = p.plot_colorbar(right_of=p.axes[3])

Using a cluster as functional ROI

Often it is desirable to summarize values in a cluster. This is especially useful in more complex designs. For example, after finding a signficant interaction effect in an ANOVA, one might want to follow up with a pairwise test of the value in the cluster. This can often be achieved using binary masks based on the cluster. Using the cluster identified above, generate a binary mask:

mask = cluster != 0
p = plot.TopoArray(mask, cmap='Wistia', t=[0.350, 0.400, 0.450])

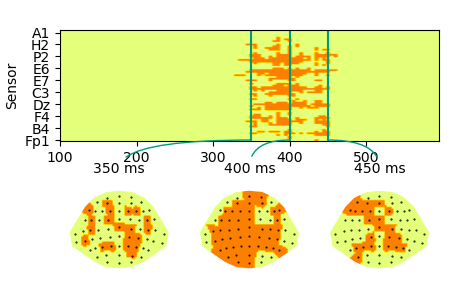
Such a spatio-temporal boolean mask can be used to extract the value in the cluster for each condition/participant. Since mask contains both time and sensor dimensions, using it with the NDVar.mean() method collapses across these dimensions and returns a scalar for each case (i.e., for each condition/subject).

ds['cluster_mean'] = ds['eeg'].mean(mask)
p = plot.Barplot('cluster_mean', 'predictability', match='subject', data=ds, test=False)

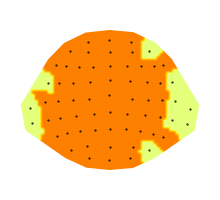
Similarly, a mask consisting of a cluster of sensors can be used to visualize the time course in that region of interest. A straight forward choice is to use all sensors that were part of the cluster (mask) at any point in time:

roi = mask.any('time')
p = plot.Topomap(roi, cmap='Wistia')

When using a mask that ony contains a sensor dimension (roi), NDVar.mean() collapses across sensors and returns a value for each time point, i.e. the time course in sensors involved in the cluster:

ds['cluster_timecourse'] = ds['eeg'].mean(roi)
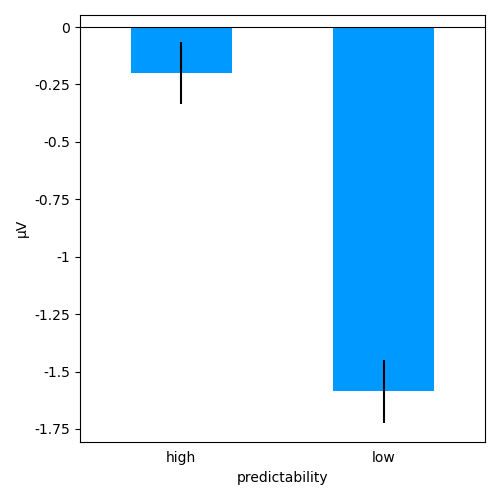
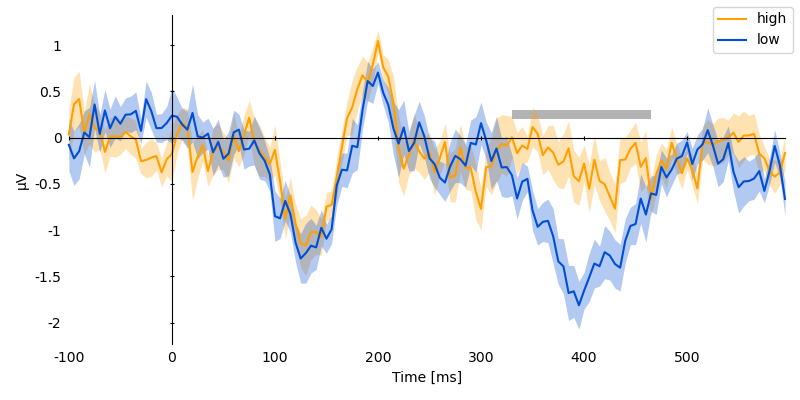
p = plot.UTSStat('cluster_timecourse', 'predictability', match='subject', data=ds, frame='t')
# mark the duration of the spatio-temporal cluster
p.set_clusters(clusters, y=0.25e-6)

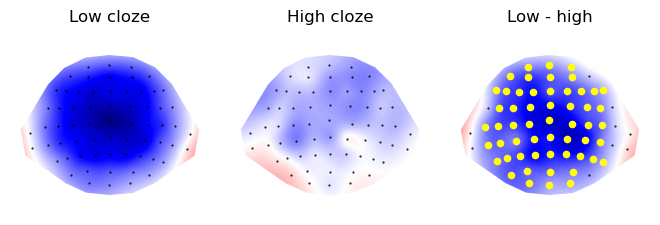
Now visualize the cluster topography, marking significant sensors:

time_window = (clusters[0, 'tstart'], clusters[0, 'tstop'])
c1_topo = res.c1_mean.mean(time=time_window)
c0_topo = res.c0_mean.mean(time=time_window)
diff_topo = res.difference.mean(time=time_window)
p = plot.Topomap([c1_topo, c0_topo, diff_topo], axtitle=['Low cloze', 'High cloze', 'Low - high'], ncol=3)
p.mark_sensors(roi, -1)

Temporal cluster based test

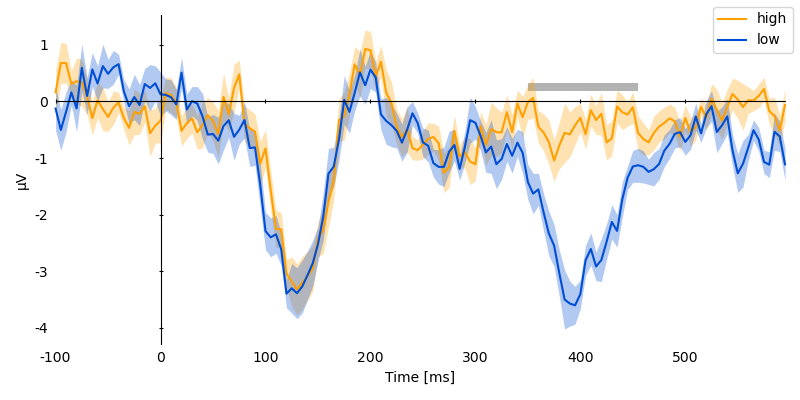
Alternatively, if a spatial region of interest exists, a univariate time course can be extracted and submitted to a temporal cluster based test. For example, the N400 is typically expected to be strong at sensor Cz:

ds['eeg_cz'] = ds['eeg'].sub(sensor='Cz')
res_timecoure = testnd.TTestRelated(
    'eeg_cz', 'predictability', 'low', 'high', match='subject', data=ds,
    pmin=0.05,  # Use uncorrected p = 0.05 as threshold for forming clusters
    tstart=0.100,  # Find clusters in the time window from 100 ...
    tstop=0.600,  # ... to 600 ms
)
clusters = res_timecoure.find_clusters(0.05)
clusters

p = plot.UTSStat('eeg_cz', 'predictability', match='subject', data=ds, frame='t')
p.set_clusters(clusters, y=0.25e-6)

Permutation test:   0%|          | 0/1023 [00:00<?, ? permutations/s]
Permutation test:  32%|███▏      | 324/1023 [00:00<00:00, 3235.44 permutations/s]
Permutation test:  67%|██████▋   | 687/1023 [00:00<00:00, 3466.81 permutations/s]
Permutation test: 100%|██████████| 1023/1023 [00:00<00:00, 3611.48 permutations/s]